Options and Real Options
Options and Real Options model consists of an Excel model which presents a valuation framework calculation for options. The calculations can be applied to both call options and put options, split into European and American options.
The Black and Scholes method is used for the valuation of the European options, while the binomial method is used for the valuation of the American options.
So, a quick overview of the model, in the contents tab you can see the structure of the model and by clicking on any of the headlines to be redirected to the relevant worksheet.
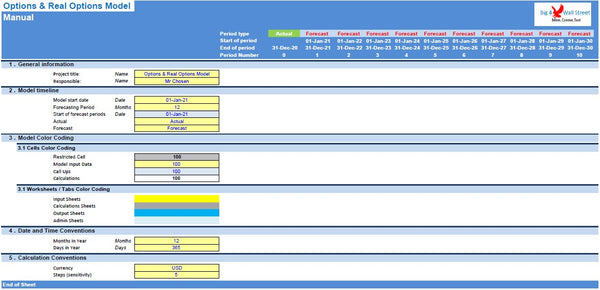
On the manual tab you can feed the general information for the model such as: model name, responsible, timeline of the model and date and currency conventions.
Additionally, there is a description of the color coding of the model in the same tab. Inputs are always depicted with a yellow fill and blue letters, call up (that is direct links from other cells) are filled in light blue with blue letters while calculations are depicted with white fill and black characters. Grey cells are restricted cells which you must not change.
There is also a color coding for the various tabs of the model. Yellow tabs are mostly assumptions tabs, grey tabs are calculations tabs, blue tabs are outputs tabs (that is effectively results or graphs) and finally light blue tabs are admin tabs (for example: the cover page, and contents).
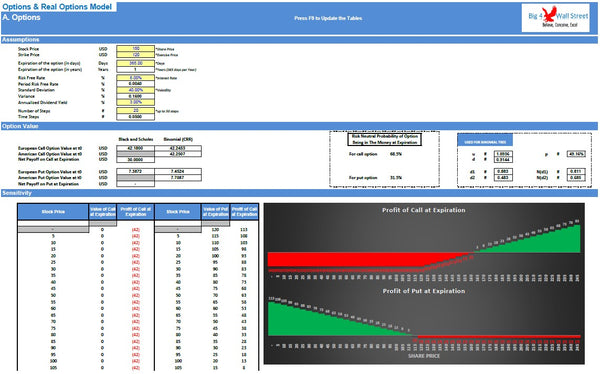
On the tab "Options", the user can set the various inputs for the option valuation, such as the stock price, strike price, expiration of the option, risk free rate, standard deviation, dividend yield, and the number of steps.
The option value is calculated here for both the Call Option and the Put Option. The American option values are calculated through binomial trees based on the methodology of Cox-Ross-Rubinstein, which can be found on the next tab. In this tab, we first calculate the value of the underlying asset and then we can calculate the value of both American and European options for both call and puts.
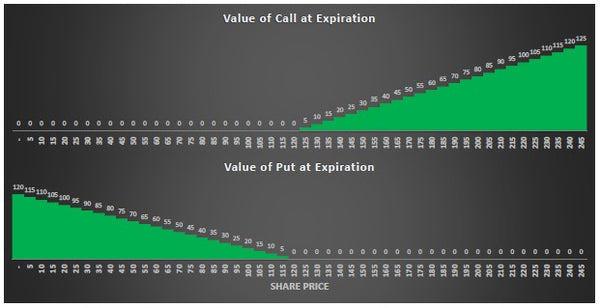
Going back to the "Options" tab, a sensitivity on the stock price is performed for both put and calls, from this sensitivity the value as well as the profit of the option at expiration is calculated.
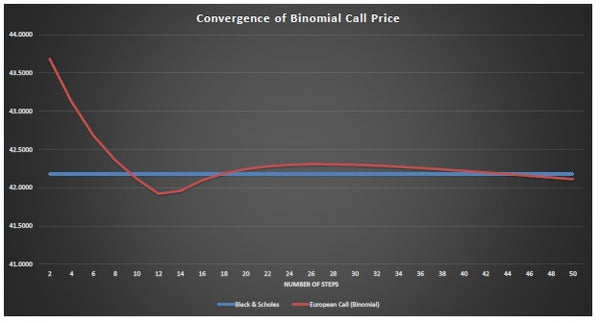
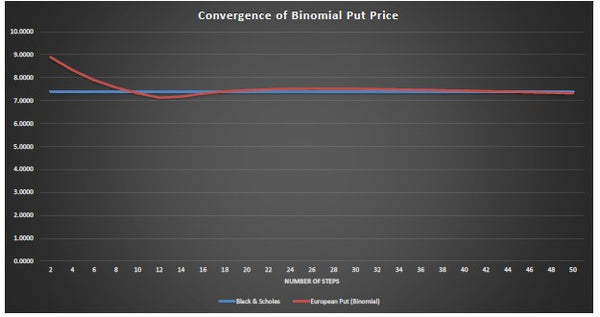
Finally, on this tab, is the convergence of the valuation price of the European option calculated through the binomial model, to the Black and Scholes price.
Moving on we can apply the option valuation logic to real world cases, which are called real options. We consider the following cases:
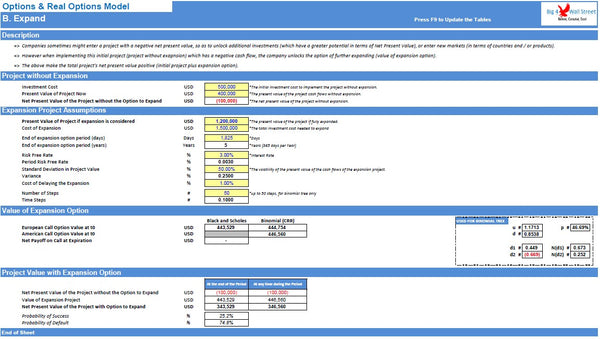
- An expansion option: sometimes a project must be a series of expansion investments, instead of a single initial investment. Effectively the initial investment might be negative from a net present value point of view, but the full expansion project might be significantly positive. An example might be Uber for a single town versus Uber for several countries.
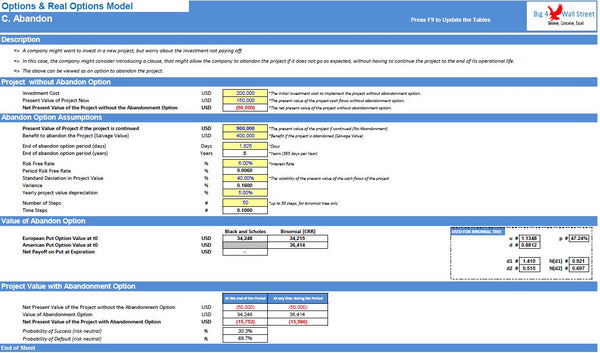
- An abandonment option: conceptually this states that a project which has an exit clause (either contractually or real) might have more value than a project without the exit possibility. The terms of this clause can be valued through an option. As soon as you introduce an exit option, the project might be worth trying.
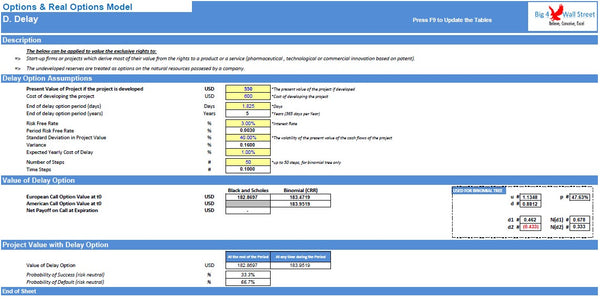
- The option to delay: a project that is negative from a net present value perspective now, might become more valuable in the future. This requires some exclusive rights the asset, and thus high barriers to entry to keep this option valuable. An example would be a land rich in natural resources which might not have value now, due to low prices, but might have value in the future if natural resources prices go up.
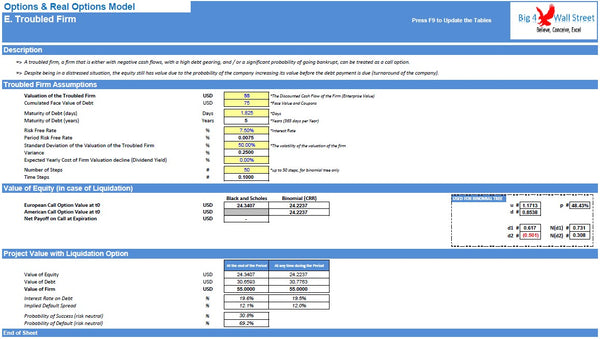
- Finally, the last real option application presented is the value of a company in financial distress. Despite the value of the distressed company being negative now, the equity still has value if we consider that there is a chance that the company succeeds in its restructuring / turnaround, and as a result can continue servicing its debt, and operating normally.